重大新闻!全世界绝无仅有的、一题十二解七十二变的横式算法横空出世。它向传统竖式算法发起全面挑战。横竖兼教,势在必行。
少年智则国智,少年强则国强,少年进步则国进步!
为了您的孩子能够冠盖群伦,为了您的学生能够茁壮成材,为了更多的孩子跨入天才行列,更为了中国教育事业的蓬勃发展。请您静下心来,听我讲一讲横式算法的教学价值和重大社会意义。
首先,横式算法不是用来提升计算速度的工具,而是铸造天才思维的手段。
这是它与竖式算法最大的不同。
横式算法是一种新型的横向笔算法。它缘于数学,又超脱于数学,它对孩子们思维模式的锻造与升华,可惠及各个学科各个领域。
请看这张横式算法五维立体思维构图:
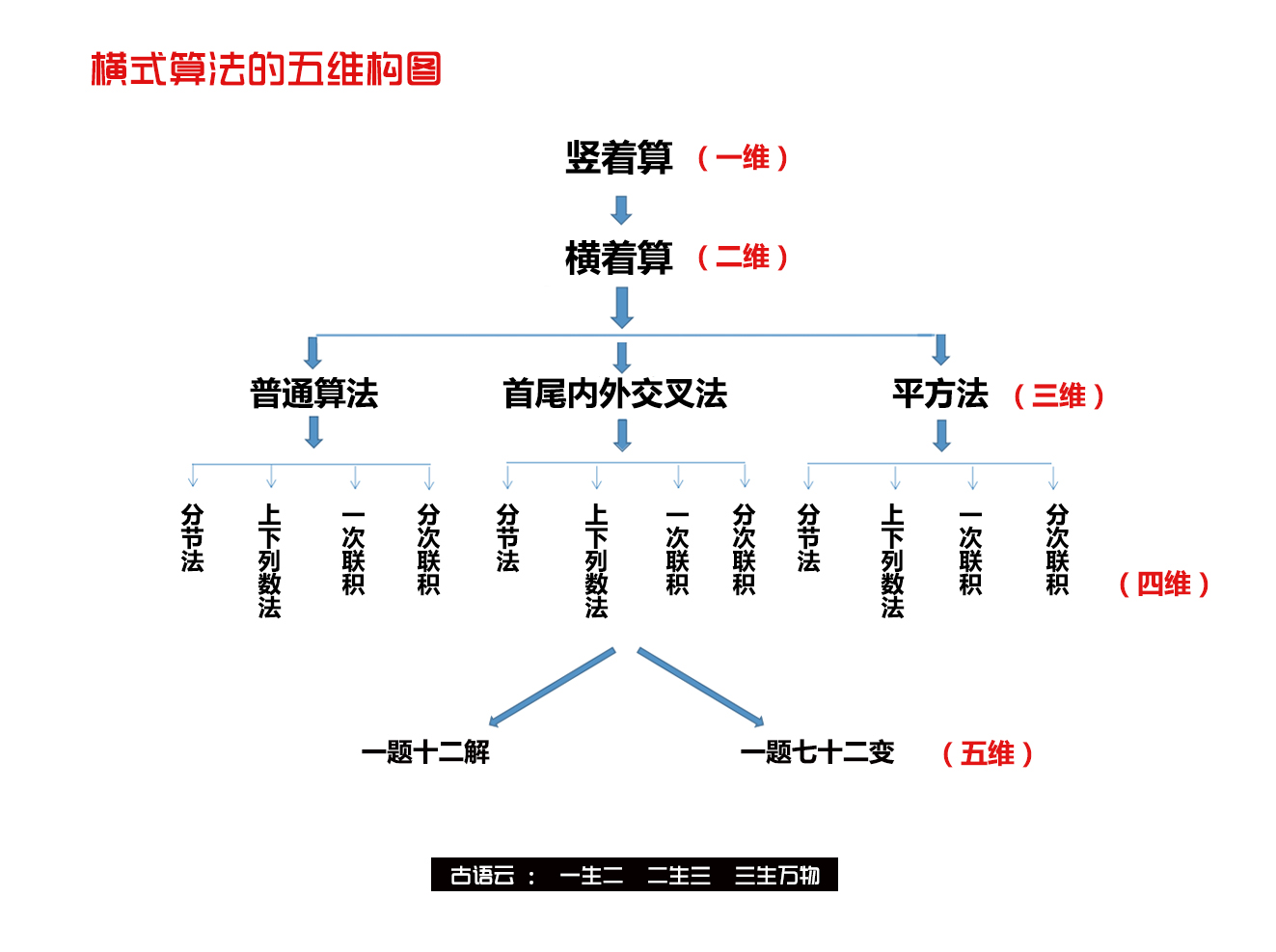
通过这个图,大家能够直观地了解一题十二解七十二变的形成过程,看到天才思维是如何诞生的。
横式算法独具三大特色:一题十二解、一题七十二变、天才核心素质的培养。
请听我慢慢道来。
第一大特色:一题十二解。
以786×786为例,它的十二种横式解法如下:
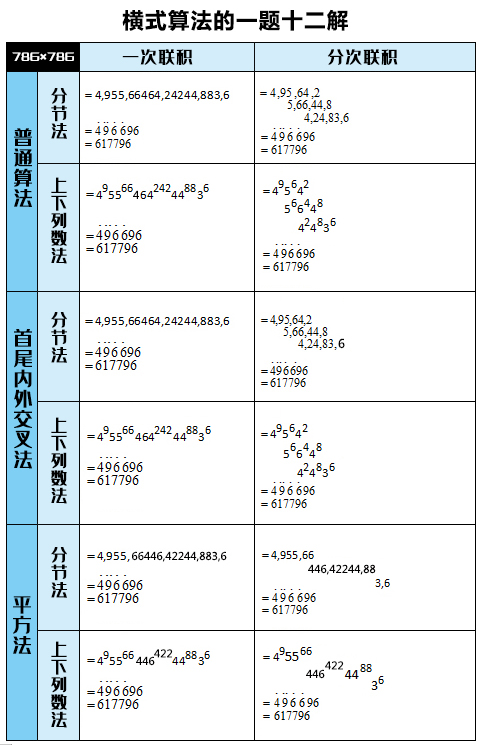
横算十二解能大大激发孩子的想象力和创造力,让孩子学会运用立体思维,从无到有、高屋建瓴地解决问题。不仅在数学领域,孩子在未来的学习、工作、生活中遇到各类难题时,都能灵犀一动、另辟蹊径、纵横无碍、八面玲珑。
我们可以看到,横式算法的思维方式是立体的、跳跃的、发散的、全视角的。它通过变竖式为横式,跨出了惊艳的第一步,跳出了固有思维和传统竖算的框架,开创了一个新的算法世界。
它又在横式的基础上衍生出三种算法,又在每种算法的基础上开发出了四种表现形式,并通过这三种算法和四种表现形式的组合,形成了横式算法独特的一题十二解。
这十二解充分展现了从无到有、一生二、二生三、三生万物的普世哲理,每一解都是创新的过程,每一个解题环节都贯穿着跳跃的、积极的、主动的思维方式。
在这种天才立体思维的引导下,孩子的灵性会被大大激发,而横式算法的妙处还不止如此。
试问,传统的竖式算法有这样的能力吗?
竖式算法,经年累月的一题一解的线性思维,只会让孩子们失去思考的主动性、积极性,丧失学习兴趣。而长期的思维固化,必然磨灭孩子的灵性,致使想像力和创造力匮乏。
我们岂能任由孩子受到这样的伤害?
有人会说:也许通过后期的学习,可以弥补这些弊病?
可是,已被固化的低阶思维,怎能轻易改变?
第二大特色:七十二变,赋予孩子极其重要的变通能力。
何为七十二变?横式算法的三种算法和四种表现形式就是七要素,将这七要素进行不同的排列组合,就形成了奇妙的一题七十二变。

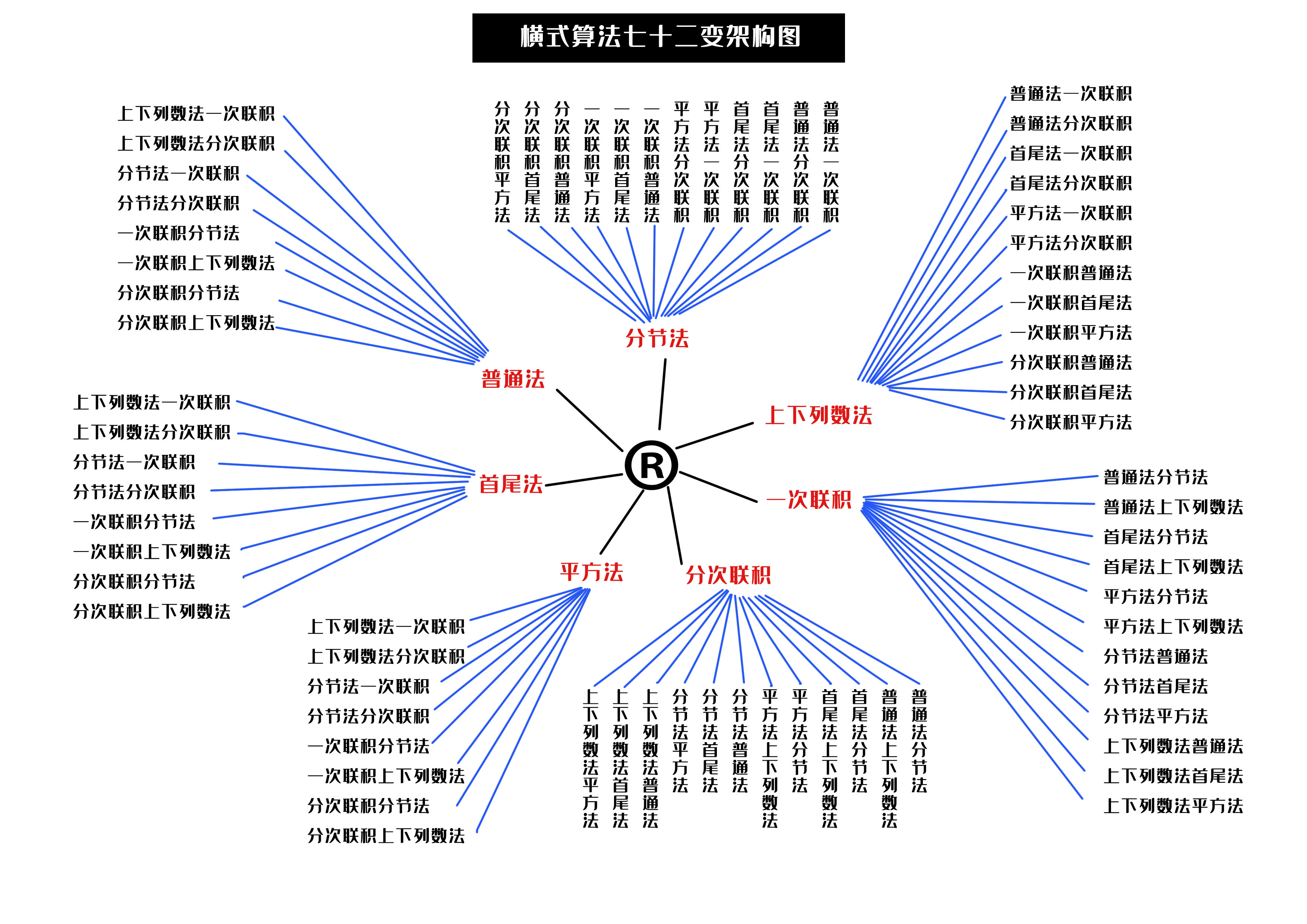
无数的学者曾经论述过:变通是生活中最重要的能力。
而横式算法的七十二变,正是开悟你的变通力。
咱们以古代故事田忌赛马为例,这个故事是一个一题三要素的范例。三要素就是上马、中马、下马,把这三要素进行不同的排列组合,得出的方案有六种,只有一种会让比赛稳赢。
即:上马对中马、中马对下马、下马对上马。
而齐国大臣田忌就是因为不懂这种排列组合,险些让齐国在这场外交事件中颜面扫地。
而孙膑帮他将现有的三要素重新排列组合,一举锁定了胜局。
可见,玩转三要素6个变化,就可以扭转乾坤。
更何况掌握了七十二变?
第三大特色:天才核心素质的培养。
横式算法又名“天才儿童量产孵化器”,您是否认为言过其实?
关于这个问题,我们先聊聊什么是天才。
请看这张图:

国家需要的是人才、天才,而不是庸才。
从思维层面讲,天才与普通人的区别,就是思维模式的区别。再看下面这张图,天才的思维高度,至少要超越三维,直至五维。
 著名的钱学森先生曾有一问,“为什么我们的学校培养不出杰出的人才”?
著名的钱学森先生曾有一问,“为什么我们的学校培养不出杰出的人才”?
请大家想一想,在儿童最重要的思维养成阶段,如果常年被传统竖式算法一题一解的线性思维所束缚,那么孩子的想像力和创造力何来?孩子的变通能力何来?天才儿童何来?
那么,如果孩子们拥有了想像力、创造力、变通力,但却马马虎虎,缺乏专注力和耐力,他还能成为天才吗?
不能!
要想成为天才,不仅需要想象力,创造力,变通力,还必须具备天才的核心素质。
即:专注力、耐力、和强大的自信。
这些都是竖式算法无法实现的,而横式算法却能全部给予。
一题十二解七十二变的解题过程,就是这些核心素质最好的培养皿。
横式算法的解题特点是:恰到好处的难。
例如下面这道题的横式解法之一:
628×395
=18 5064 312480 7102 40
=248060
大家可以看到,它的每一个解题环节是相对简单的,但需要的综合素质却很高,因为每一个环节都是跳跃的、发散的,每一个环节都不能出错。
比如:位置摆放合乎逻辑、数字相加必须精准、空间预留要有前瞻性。
所以要求孩子们必须要做到思维慎密、高度专注、脑算精确、具备大局观等等,这些核心素质都具备,才能正确的做完一道题。所以横式算法对核心素质的培养直接且有效,绝非传统竖算可比。
所以,如果孩子在一题十二解和一题七十二变中铸就了天才思维能力,同时又在习练过程中形成了天才的核心素质,那么他怎能不出类拔萃?
眼放长远。如果全中国的孩子都在思维模式和核心素质上有了一个质的飞跃,那么中国的天才量产岂不是指日可待?中国的繁荣富强岂不是更上一层楼?
这就是横式算法的重大社会意义。
我画了一张横式算法与传统竖算的优劣对比图,请大家评判。

综上所述:采纳横算,横竖兼教,意义深远,势在必行!
期待与广大教育工作者、数学爱好者、以及所有关心中国教育事业的有识之士探讨交流,欢迎一切批评建议。
中国的横式算法,终将照亮世界,映画人类未来!